On Maximal Self-Avoiding Walks
Given a k × n grid, a self-avoiding walk (SAW) on that grid is a connected path that never touches the same square more than once and never doubles back on itself (note that some sources make the convention that the path is drawn on the edges of the grid from vertex to vertex, but here I will make the convention that the path connects the centres of the squares that the grid forms). I will define a maximal self-avoiding walk to be a self-avoiding walk that touches every square of the grid on which it resides. One natural question that we can ask in this setting is “How many maximal self-avoiding walks are there on a k × n grid?”
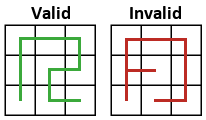 Before proceeding, let’s simplify things slightly by making the restriction that the maximal self-avoiding walks must start in the bottom-left corner of the grid (this restriction leaves us with the walks that are known as “Greek-key tours”). Let f(k, n) denote the number of maximal self-avoiding walks on a k × n grid. Unfortunately, finding an expression for f(k, n) in complete generality seems to be out of reach, so we will instead try to answer the question for certain fixed values of k.
Before proceeding, let’s simplify things slightly by making the restriction that the maximal self-avoiding walks must start in the bottom-left corner of the grid (this restriction leaves us with the walks that are known as “Greek-key tours”). Let f(k, n) denote the number of maximal self-avoiding walks on a k × n grid. Unfortunately, finding an expression for f(k, n) in complete generality seems to be out of reach, so we will instead try to answer the question for certain fixed values of k.
Case 1: k = 1
Regardless of n, there is clearly only one maximal self-avoiding walk in this case: a straight line. Thus, f(1, n) = 1 regardless of the value of n.
Case 2: k = 2
It is not difficult to prove (by induction, for example) that f(2, n) = n.
Case 3: k = 3
This is the first case whose solution does not seem trivial. It is well-known (by people who have looked at this problem, anyways) that the number of maximal self-avoiding walks on a 3 × n grid for n = 1, 2, … is 1, 3, 8, 17, 38, … (Sloane’s A046994). This sequence is defined by the following recurrence relations:
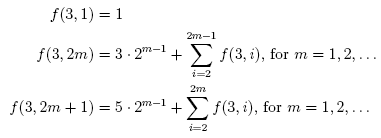
Well, from these recurrence relations we can derive the following closed form expression for f(3, n):
It may be worth noting that this formula can be simplified significantly if you consider the case when n is odd separately from the case when n is even, and write f(3, n) as a branch function.
Case 4: k = 4
The number of maximal self-avoiding walks on a 4 × n grid for n = 1, 2, … is 1, 4, 17, 52, 160, … (Sloane’s A046995), but to date no simple closed-form formula for f(4, n) has been found. In 2003, Dean Hickerson proposed the following recurrence relation to define f(4, n), which holds at least for the first 25 terms of the sequence:
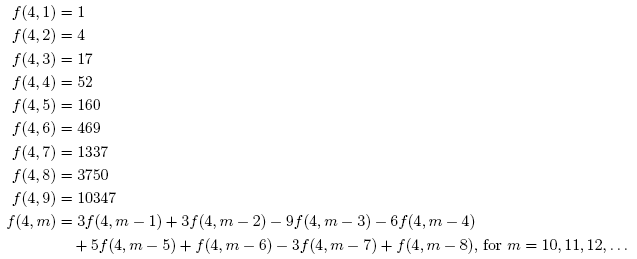
While it is possible to derive a closed-form formula for f(4, n) from the above recurrence relation using standard difference equation techniques, the formula is extremely long and cumbersome. One piece of information that we can extract from the closed-form formula (which I won’t write out here) is that f(4, n) ∈ O(2.539n).
Case 5: k ≥ 5
It is now clear that this problem grows very large very quickly, and proceeding in this manner may not be (realistically) feasible. Not much is known about f(k, n) when both k and n are greater than or equal to 5. The best approach in this case is likely that of brute force.
Computing the Number of Maximal SAWs
Here I provide two programs for computing the number of maximal SAWs on a grid of your chosen size. It is recommended that you use the C script rather than the Visual Basic program, as the C script is much faster.
If the Visual Basic file below gives you an error message when you try to run it, you may need to download and install the Visual Basic 6.0 run time files. Click here to download these files. As far as I know, this program should work on Windows 98, ME, 2000, XP and Vista, but I can’t make any guarantees about its compatability.
Download:
- Maximal SAW Calculator in Visual Basic [Windows exe — 28.0kB]
- Maximal SAW Calculator in C [Windows exe — 17.6kB]
- Maximal SAW Calculator in C source code [zip — 1.06kB]
Maximal SAW Table of Values
This is a table giving the number of maximal SAWs on a k × n grid. Several of the values in the table below were calculated using the above software — the cells that have “?” in them correspond to values that are currently unknown due to computational limits. Note that there is trivially symmetry across the main diagonal of the table. I apologize for the unreadably small font.
| k\n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | General Term |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | n |
| 3 | 1 | 3 | 8 | 17 | 38 | 78 | 164 | 332 | 680 | 1368 | Sloane’s A046994 |
| 4 | 1 | 4 | 17 | 52 | 160 | 469 | 1337 | 3750 | 10347 | 28249 | Sloane’s A046995 |
| 5 | 1 | 5 | 38 | 160 | 824 | 3501 | 16262 | 68591 | 304177 | 1276805 | Sloane’s A145156 |
| 6 | 1 | 6 | 78 | 469 | 3501 | 22144 | 144476 | 899432 | 5585508 | 34092855 | Sloane’s A160240 |
| 7 | 1 | 7 | 164 | 1337 | 16262 | 144476 | 1510446 | 13506023 | 132712481 | 1185979605 | Sloane’s A160241 |
| 8 | 1 | 8 | 332 | 3750 | 68591 | 899432 | 13506023 | 180160012 | ? | ? | ? |
| 9 | 1 | 9 | 680 | 10347 | 304177 | 5585508 | 132712481 | ? | ? | ? | ? |
| 10 | 1 | 10 | 1368 | 28249 | 1276805 | 34092855 | 1185979605 | ? | ? | ? | ? |
| n × n grid: | Sloane’s A145157 | ||||||||||
Related Links:
- ‘Greek-key’ tours on 3 × n chessboards — A mathforum.org posting by Thomas Womack in April 1999 about maximal SAWs.
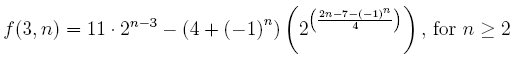
Some people may disagree about the impossibility of figuring out a general case formula for this as well! Of course, those people should probably put their money where their mouth is and actually attempt to make further progress some time, maybe…
I am definitely in the group of people who think that finding a general formula for arbitrary k and n isn’t realistically possible for this problem as well, which is why I coded those scripts 😉 A formula could likely be derived by a very devoted person for the k = 4 and k = 5 cases, but they’d be horrendously long and not particularly informative.
I might take another look at the lake counting problem soon, but it still seems to me that as the lakes get bigger and bigger, more and more ways of things “going wrong” crop up, for the most part in rather unpredictable ways, which makes obtaining recurrence relations extremely difficult.
The method of relating lakes to polyominoes seems by far the most promising approach so far, so I’ll have a look at that again soon, I suppose.
You know, your remark about it being impossible makes me want to do it ten times more, of course! I get some sort of accolades if I’m successful, right?
Of course! You get your name in the OEIS and a personal “Elithrion was right” post from me, earning you internet accolades from all three readers of my blog 😉
Maybe it’s worth pointing out that for the case k=3 the following recurrence relation also seems to hold:
f(2)=3
f(3)=8
f(4)=17
f(n+3) = 2*f(n+2) + 2*f(n+1) – 4*f(n)